/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Udowodnij...

Zadanie nr 8191904

Dodaj do ulubionych
Dodaj do rozwiązanych

Dwusieczna kąta ostrego 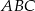ABC przecina przyprostokątną 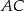AC trójkąta prostokątnego 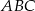ABC w punkcie D .

PIC

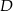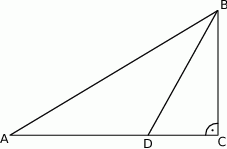
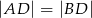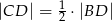Udowodnij, że jeżeli |AD | = |BD | , to |CD | = 12 ⋅ |BD | .

Rozwiązanie

Trójkąt 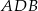ADB jest równoramienny, więc

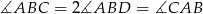
∡ABC = 2∡ABD = ∡CAB

Stąd

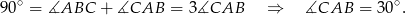
∘ ∘ 90 = ∡ABC + ∡CAB = 3∡CAB ⇒ ∡CAB = 30 .

To oznacza, że

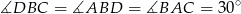
∘ ∡DBC = ∡ABD = ∡BAC = 30

oraz

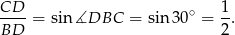
CD-- ∘ 1- BD = sin∡DBC = sin3 0 = 2 .

Oczywiście zamiast używać funkcji trygonometrycznych mogliśmy też zauważyć, że trójkąt 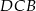DCB jest połówką trójkąta równobocznego.

Wersja PDF