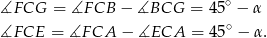Zadanie nr 9233754
Udowodnij, że w trójkącie prostokątnym dwusieczna kąta prostego dzieli na połowy kąt zawarty między środkową, a wysokością opuszczoną z wierzchołka kąta prostego.
Rozwiązanie
Oznaczmy przez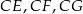 
kolejno: środkową, dwusieczną i wysokość trójkąta prostokątnego 
.
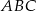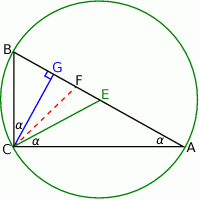
Zauważmy, że okrąg o średnicy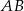 
przechodzi przez punkt 
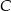(bo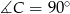 
). To oznacza, że środek 
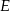przeciwprostokątnej jest środkiem okręgu opisanego na trójkącie 
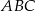. W szczególności
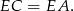
W takim razie trójkąt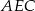 
jest równoramienny i
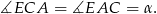
Ponadto
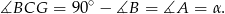
Zatem
