/Szkoła średnia/Zadania maturalne/Matura 2012/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 24 marca 2012 Czas pracy: 180 minut
Rozwiąż nierówność 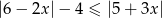 .
.
Uzasadnij, że 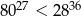 .
.
Wykaż, że nie istnieje para liczb 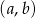 spełniająca układ równań
spełniająca układ równań 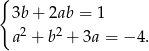
Wyznacz wszystkie rozwiązania równania 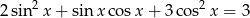 należące do przedziału
należące do przedziału 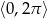 .
.
Wyznacz wszystkie wartości parametru 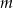 , dla których suma odwrotności pierwiastków równania
, dla których suma odwrotności pierwiastków równania
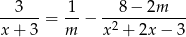
jest równa 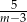 .
.
Suma trzech liczb tworzących ciąg geometryczny jest równa 63, a ich iloczyn jest równy 5832. Wyznacz ten ciąg.
W trójkącie 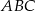 , w którym
, w którym 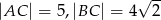 i
i 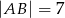 na boku
na boku 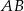 wybrano taki punkt
wybrano taki punkt 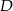 , że
, że 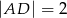 . Oblicz sinus kąta
. Oblicz sinus kąta 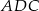 .
.
Podstawą graniastosłupa prostego jest trójkąt równoramienny o ramionach długości  . Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Jakie powinny być długości pozostałych krawędzi graniastosłupa, aby jego objętość była największa?
. Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Jakie powinny być długości pozostałych krawędzi graniastosłupa, aby jego objętość była największa?
Dane są punkty 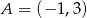 i
i 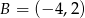 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 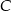 na prostej
na prostej 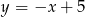 tak, aby pole trójkąta
tak, aby pole trójkąta 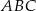 było równe 7.
było równe 7.
Ze zbioru liczb 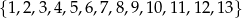 losujemy bez zwracania 4 liczby. Oblicz jakie jest prawdopodobieństwo, że wśród 4 otrzymanych liczb jest dokładnie jedna para liczb o sumie równej 14.
losujemy bez zwracania 4 liczby. Oblicz jakie jest prawdopodobieństwo, że wśród 4 otrzymanych liczb jest dokładnie jedna para liczb o sumie równej 14.
Stosunek pola powierzchni bocznej stożka do pola przekroju osiowego tego stożka jest równy 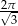 . Oblicz kąt rozwarcia stożka.
. Oblicz kąt rozwarcia stożka.

