/Szkoła podstawowa/Zadania testowe

Zadanie nr 1290258

Dodaj do ulubionych
Dodaj do rozwiązanych

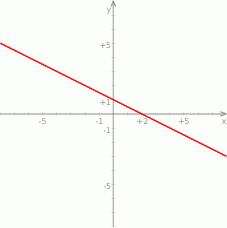
Wskaż wzór funkcji, której wykres przedstawiono na poniższym rysunku.

PIC

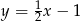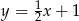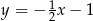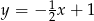
A) y = 12x − 1 B) y = 12x + 1 C) y = − 1x− 1 2 D) y = − 1x + 1 2

Rozwiązanie

Z podanego wykresu widać, że wykres funkcji przechodzi przez punkty 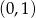(0,1) i (2 ,0) .

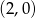Sposób I

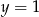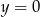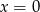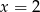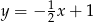Sprawdzamy, w którym wzorów otrzymamy y = 1 i y = 0 po podstawieniu odpowiednio x = 0 i x = 2 . Gdy to zrobimy, okaże się, że tak jest tylko w przypadku funkcji: y = − 12x+ 1 .

Sposób II

Ponieważ dany wykres jest linią prostą, jest to wykres funkcji liniowej postaci 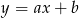y = ax+ b . Podstawiamy teraz współrzędne zauważonych wcześniej punktów wykresu i mamy

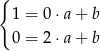
{ 1 = 0 ⋅a+ b 0 = 2 ⋅a+ b

Z pierwszego równania mamy 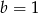b = 1 , więc drugie równanie przybiera postać

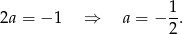
1 2a = − 1 ⇒ a = − -. 2

Jest to więc funkcja 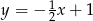y = − 1x + 1 2 .

Sposób III

Z danego rysunku widać, że mamy do czynienia z funkcją malejącą, więc jest to albo funkcja 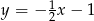y = − 1x− 1 2 , albo 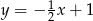y = − 1x+ 1 2 . Sprawdzamy teraz, że tylko druga z nich przechodzi przez punkt (0,1 ) .  
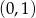Odpowiedź: D

Wersja PDF