Zadanie nr 2377342
Każdy z dwóch jednakowych sześcianów o krawędzi 2 cm podzielono na mniejsze sześciany o krawędzi 1 cm. Czy z otrzymanych w ten sposób małych sześciennych kostek można ułożyć jeden pełny sześcian, tak by wszystkie kostki były wykorzystane? Wybierz odpowiedź T lub N i jej uzasadnienie wybrane spośród A, B, C, D.
| Tak | Nie |
| ponieważ | |
| A) | Liczba małych kostek nie jest podzielna przez 3. |
| B) | Liczba małych kostek jest potęgą liczby 2. |
| C) | Liczba małych kostek jest drugą potęgą liczby naturalnej. |
| D) | Liczba małych kostek nie jest trzecią potęgą liczby naturalnej. |
Rozwiązanie
Każdy z sześcianów podzielono na 8 kostek, więc w sumie mamy 16 kostek.
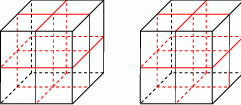
Zauważmy teraz, że gdyby z tych kostek można było zbudować sześcian, to objętość tego sześcianu byłaby sześcianem liczby naturalnej (bo krawędź byłaby liczbą naturalną). To jednak jest niemożliwe, bo 16 nie jest sześcianem liczby naturalnej.
Odpowiedź: N, D

