Zadanie nr 2696886
Na okręgu o środku w punkcie 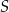 zaznaczono punkty
zaznaczono punkty 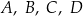 , a następnie narysowano odcinki
, a następnie narysowano odcinki 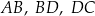 oraz
oraz 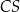 (zobacz rysunek).
(zobacz rysunek).

Trójkąt 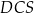 A/B równoramienny.
A/B równoramienny.
A) jest B) nie jest
Długość odcinka 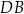 jest równa C/D.
jest równa C/D.
C) sumie długości odcinków 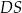 i
i 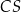 D) długości odcinka
D) długości odcinka 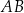
Rozwiązanie
Każdy z odcinków 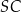 i
i 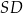 jest promieniem danego okręgu, więc mają one tą samą długość. W szczególności trójkąt
jest promieniem danego okręgu, więc mają one tą samą długość. W szczególności trójkąt 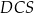 jest równoramienny.
jest równoramienny.
Odcinek 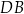 przechodzi przez środek okręgu, jest więc jego średnicą. W szczególności jest dwa razy dłuższy od promienia okręgu. Zatem
przechodzi przez środek okręgu, jest więc jego średnicą. W szczególności jest dwa razy dłuższy od promienia okręgu. Zatem
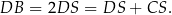
Odpowiedź: A, C

