Zadanie nr 3047099
Prostokąt o wymiarach 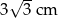 i
i 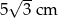 podzielono na 15 jednakowych kwadratów. Pole jednego kwadratu jest równe
podzielono na 15 jednakowych kwadratów. Pole jednego kwadratu jest równe
A) 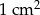 B)
B) 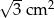 C)
C) 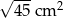 D)
D) 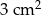
Rozwiązanie
Sposób I
Pole danego prostokąta jest równe
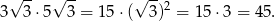
W takim razie pole jednego z kwadratów na który podzielono prostokąt jest równe
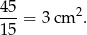
Sposób II
Prostokąt o bokach długości 3 cm i 5 cm składa się z 15 kwadratów o polu 1. Jeżeli teraz każdy z boków tego prostokąta pomnożymy przez 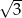 , to otrzymamy prostokąt, o którym mowa w treści zadania. Składa się on więc z 15 kwadratów o boku
, to otrzymamy prostokąt, o którym mowa w treści zadania. Składa się on więc z 15 kwadratów o boku 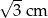 . Każdy z tych kwadratów ma więc pole
. Każdy z tych kwadratów ma więc pole 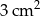 .
.
Odpowiedź: D

