Zadanie nr 3324053
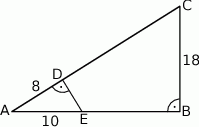
Na bokach 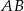 i
i 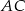 trójkąta prostokątnego
trójkąta prostokątnego 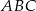 wybrano punkty
wybrano punkty 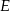 i
i 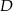 tak, że
tak, że 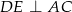 ,
, 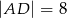 i
i 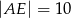 . Przyprostokątna
. Przyprostokątna  trójkąta
trójkąta  ma długość 18.
ma długość 18.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
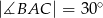 | P | F |
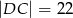 | P | F |
Rozwiązanie
Na mocy twierdzenia Pitagorasa
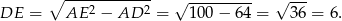
Gdyby 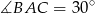 , to trójkąt
, to trójkąt 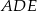 byłby połówką trójkąta równobocznego. Ale wtedy musiałoby być
byłby połówką trójkąta równobocznego. Ale wtedy musiałoby być 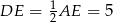 , co nie jest prawdą.
, co nie jest prawdą.
Trójkąty 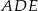 i
i 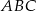 są podobne i znamy ich skalę podobieństwa
są podobne i znamy ich skalę podobieństwa
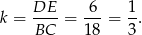
Zatem
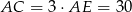
i 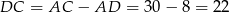 .
.
Odpowiedź: F, P

