Zadanie nr 3822398
Jeżeli 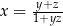 i
i 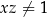 , to
, to
A) 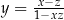 B)
B) 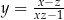 C)
C) 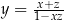 D)
D) 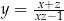
Rozwiązanie
Wyznaczymy z podanego wzoru 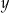 .
.
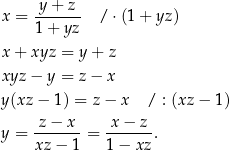
Odpowiedź: A
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Jeżeli 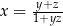 i
i 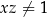 , to
, to
A) 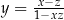 B)
B) 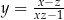 C)
C) 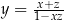 D)
D) 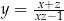
Wyznaczymy z podanego wzoru 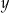 .
.
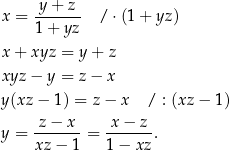
Odpowiedź: A
