/Szkoła podstawowa/Zadania testowe

Zadanie nr 4143920

Dodaj do ulubionych
Dodaj do rozwiązanych

Na giełdzie kupiono tę samą liczbę akcji dwóch przedsiębiorstw, przy czym średnia cena zakupu jednej akcji drugiego przedsiębiorstwa była dwa razy wyższa od średniej ceny akcji pierwszego przedsiębiorstwa. Ile średnio zapłacono za jedną akcję drugiego przedsiębiorstwa, jeżeli średnia cena zakupu wszystkich akcji wyniosła 90 zł?
A) 30 zł B) 60 zł C) 90 zł D) 120 zł

Rozwiązanie

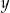Powiedzmy, że kupiono n akcji każdego z przedsiębiorstw, przy czym za akcje pierwszego z nich zapłacono x , a za akcje drugiego y złotych. Wiemy, że średnia cena zakupu akcji drugiego przedsiębiorstwa była dwa razy wyższa od średniej ceny zakupu akcji pierwszego przedsiębiorstwa, więc

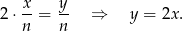
x- y- 2 ⋅n = n ⇒ y = 2x .

Korzystamy teraz z podanej informacji o średniej cenie zakupu wszystkich akcji.

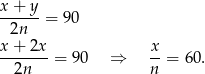
x-+-y- 2n = 90 x + 2x x -------= 90 ⇒ --= 60 . 2n n

Średnia cena zakupu akcji drugiego przedsiębiorstwa jest więc równa

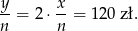
y-= 2 ⋅ x = 120 zł. n n

 
Odpowiedź: D

Wersja PDF