/Szkoła podstawowa/Zadania testowe

Zadanie nr 4478111

Dodaj do ulubionych
Dodaj do rozwiązanych

Obwód prostokąta jest równy 32 cm, a jeden z jego boków jest 3 razy dłuższy od drugiego boku. Pole tego prostokąta jest równe:
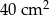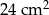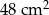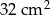
A) 40 cm 2 B) 24 cm 2 C) 48 cm 2 D) 32 cm 2

Rozwiązanie

Sposób I

Oznaczamy długości boków prostokąta przez 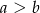a > b . Z podanych informacji otrzymujemy układ równań

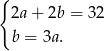
{ 2a + 2b = 32 b = 3a.

Podstawiamy 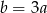b = 3a w pierwszym równaniu.

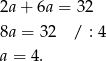
2a+ 6a = 32 8a = 32 / : 4 a = 4.

Zatem 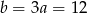b = 3a = 12 i pole jest równe

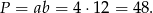
P = ab = 4 ⋅12 = 48.

Sposób II

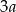Z treści zadania wynika, że długości boków prostokąta możemy oznaczyć przez a i 3a . Z informacji o obwodzie mamy

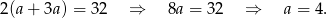
2(a+ 3a) = 32 ⇒ 8a = 32 ⇒ a = 4.

Zatem drugi bok ma długość 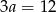3a = 1 2 i pole jest równe

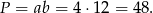
P = ab = 4 ⋅12 = 48.

 
Odpowiedź: C

Wersja PDF