Zadanie nr 5355062
Na rysunku przedstawiono czworokąt 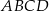 , w którym
, w którym 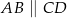 i trójkąt równoramienny
i trójkąt równoramienny 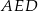 , w którym
, w którym 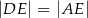 . Miara kąta
. Miara kąta 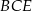 jest równa
jest równa 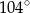 , a miara kąta
, a miara kąta 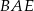 jest równa
jest równa 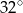 .
.
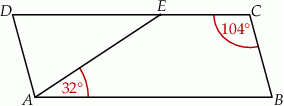
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 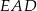 ma miarę ma miarę 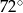 . . | P | F |
Czworokąt 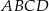 jest równoległobokiem. jest równoległobokiem. | P | F |
Rozwiązanie
Zauważmy najpierw, że
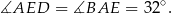
Teraz korzystamy z tego, że trójkąt 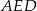 jest równoramienny
jest równoramienny
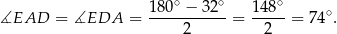
Stąd
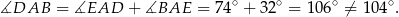
To oznacza, że proste 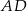 i
i 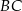 nie są równoległe.
nie są równoległe.
Odpowiedź: F, F

