Zadanie nr 5678583
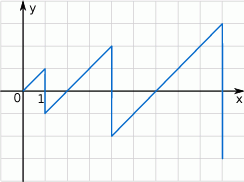
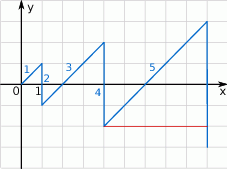
Zaczynając od punktu 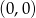 budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2.
budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Długość odcinka o numerze 5 jest równa 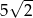 . . | P | F |
Jeżeli  jest liczbą parzystą, to długość odcinka o numerze jest liczbą parzystą, to długość odcinka o numerze 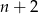 jest o 2 większa od długości odcinka o numerze jest o 2 większa od długości odcinka o numerze  . . | P | F |
Rozwiązanie
Długość piątego odcinka możemy obliczyć korzystając z twierdzenia Pitagorasa.
Liczymy
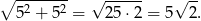
Odcinki o numerach parzystych to pionowe odcinki o długościach będących kolejnymi liczbami parzystymi, zatem rzeczywiście różnica długości dwóch kolejnych odcinków o numerach parzystych jest równa 2.
Odpowiedź: P, P

