Zadanie nr 6319684
Trójki liczb naturalnych 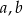 i
i  , które spełniają warunek
, które spełniają warunek 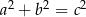 , nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
, nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
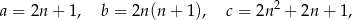
gdzie  oznacza dowolną liczbę naturalną (
oznacza dowolną liczbę naturalną (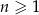 ).
).
Liczba 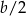 zawsze będzie A/B.
zawsze będzie A/B.
A) parzysta B) nieparzysta
Liczby 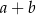 i
i  różnią się o C/D.
różnią się o C/D.
C) 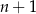 D)
D) 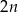
Rozwiązanie
Liczba
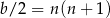
jest zawsze liczbą parzystą (dzieli się przez 2), bo albo  albo
albo 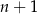 jest liczbą parzystą. Ponadto
jest liczbą parzystą. Ponadto
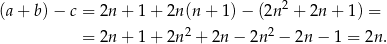
Odpowiedź: A, D

