Zadanie nr 6482461
Kąt między cięciwą 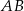 a styczną do okręgu w punkcie
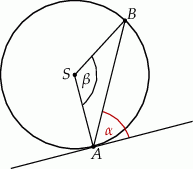
a styczną do okręgu w punkcie 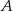 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 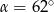 . Wówczas
. Wówczas
A) 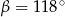 B)
B) 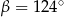 C)
C) 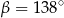 D)
D) 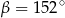
Rozwiązanie
Sposób I
Ponieważ styczna jest prostopadła do promienia 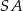 mamy
mamy
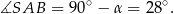
Trójkąt 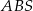 jest równoramienny, więc
jest równoramienny, więc 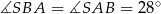 . Stąd
. Stąd
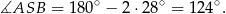
Sposób II
Na mocy twierdzenia o stycznej do okręgu (które tak naprawdę udowodniliśmy w poprzednim sposobie), zaznaczony kąt  jest równy kątowi wpisanemu opartemu na łuku
jest równy kątowi wpisanemu opartemu na łuku 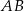 .
.
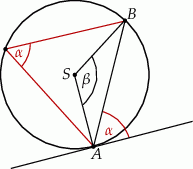
Ten kąt ma miarę równą połowie odpowiadającego kąta środkowego, czyli
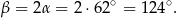
Odpowiedź: B

