Zadanie nr 6532855
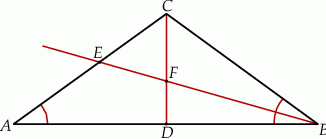
W trójkącie równoramiennym 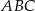 , w którym
, w którym 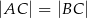 i
i 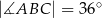 poprowadzono wysokość
poprowadzono wysokość 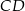 i dwusieczną kąta
i dwusieczną kąta 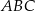 przecinającą bok
przecinającą bok 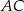 w punkcie
w punkcie 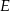 . Wysokość i dwusieczna przecinają się w punkcie
. Wysokość i dwusieczna przecinają się w punkcie 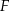 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
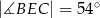 | P | F |
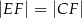 | P | F |
Rozwiązanie
Z podanych informacji wiemy, że
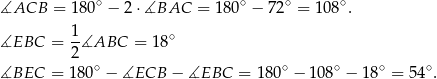
Ponadto
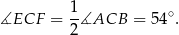
To oznacza, że trójkąt 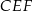 rzeczywiście jest równoramienny.
rzeczywiście jest równoramienny.
Odpowiedź: P, P

