Zadanie nr 6705104
Punkty 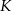 ,
, 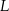 i
i 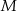 są środkami boków
są środkami boków 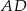 ,
, 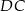 i
i 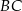 kwadratu
kwadratu 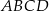 (rysunek).
(rysunek).
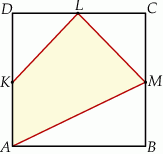
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 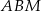 stanowi stanowi 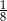 pola kwadratu pola kwadratu 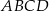 . . | P | F |
Pole czworokąta 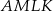 stanowi połowę pola kwadratu stanowi połowę pola kwadratu 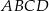 . . | P | F |
Rozwiązanie
Jeżeli oznaczymy przez  długość boku kwadratu, to pole trójkąta
długość boku kwadratu, to pole trójkąta 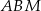 jest równe
jest równe
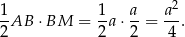
Pole to stanowi więc 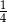 pola kwadratu.
pola kwadratu.
Podobnie obliczamy pola trójkątów 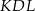 i
i 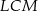
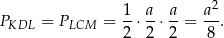
Pole czworokąta 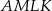 obliczamy odejmując od pola kwadratu pola trójkątów
obliczamy odejmując od pola kwadratu pola trójkątów 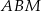 ,
, 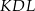 i
i 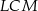 .
.
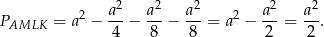
Innym sposobem uzasadnienia, że 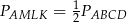 może być podział czworokąta
może być podział czworokąta 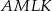 na cztery trójkąty prostokątne jak na rysunku poniżej.
na cztery trójkąty prostokątne jak na rysunku poniżej.
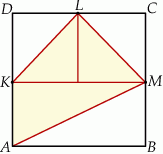
Z powyższego rysunku powinno być jasne, że suma pól zacieniowanych trójkątów jest równa sumie pól trójkątów, które nie są zacieniowane.
Odpowiedź: F, P

