Zadanie nr 6752302
Sześć różnych liczb naturalnych zapisano w kolejności od najmniejszej do największej:
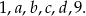
Mediana liczb: 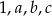 jest dwa razy mniejsza od mediany liczb
jest dwa razy mniejsza od mediany liczb 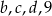 , a średnia arytmetyczna liczb
, a średnia arytmetyczna liczb 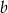 i
i  jest liczbą naturalną. Mediana liczb
jest liczbą naturalną. Mediana liczb 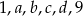 jest równa
jest równa
A) 5 B) 4 C) 6 D) 3
Rozwiązanie
Jeżeli mediana liczb 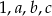 jest dwa razy mniejsza od mediany liczb
jest dwa razy mniejsza od mediany liczb 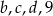 , to
, to
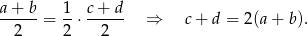
Wiemy ponadto, że liczby są różne i wypisane w kolejności rosnącej, więc największa możliwa wartość 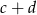 to
to 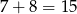 . W takim razie największa możliwa wartość
. W takim razie największa możliwa wartość 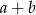 to 7. Są zatem 4 możliwości wybrania liczb
to 7. Są zatem 4 możliwości wybrania liczb  i
i 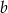
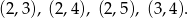
W każdym z tych przypadkach liczby  i
i 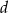 możemy dobrać tylko na jeden sposób i są one równe odpowiednio
możemy dobrać tylko na jeden sposób i są one równe odpowiednio
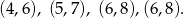
W pierwszych trzech z tych przypadków średnia 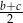 nie jest liczbą naturalną. Dane liczby muszą więc być równe
nie jest liczbą naturalną. Dane liczby muszą więc być równe
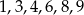
Ich mediana to 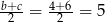 .
.
Odpowiedź: A

