Zadanie nr 7104910
Czy suma dowolnych trzech kolejnych liczb całkowitych jest podzielna przez 3? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–C.
| Tak | Nie |
| ponieważ wśród dowolnych trzech kolejnych liczb całkowitych | |
| A) | musi znajdować się liczba podzielna przez 3. |
| B) | znajdują się liczby, które dają reszty: 0, 1 i 2 przy dzieleniu przez 3. |
| C) | znajduje się liczba, która nie jest podzielna przez 3. |
Rozwiązanie
Trzy kolejne liczby całkowite możemy oznaczyć przez: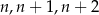 
. Ich suma jest równa
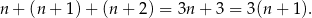
Oczywiście jest to liczba podzielna przez 3. Zauważmy też, że każda z tych trzech liczb daje inną resztę przez dzieleniu przez 3.
Odpowiedź: T, B
