Zadanie nr 7998937
Dany jest wzór opisujący pole trójkąta 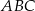 :
: 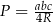 , gdzie
, gdzie 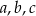 są długościami boków tego trójkąta, a
są długościami boków tego trójkąta, a 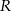 jest promieniem okręgu przechodzącego przez punkty
jest promieniem okręgu przechodzącego przez punkty 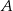 ,
, 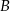 i
i 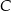 . Promień
. Promień 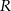 można wyrazić wzorem A/B.
można wyrazić wzorem A/B.
A) 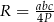 B)
B) 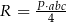
Długość boku  trójkąta
trójkąta 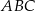 można wyrazić wzorem C/D.
można wyrazić wzorem C/D.
C) 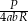 D)
D) 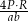
Rozwiązanie
Obliczamy z danego wzoru 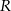 .
.
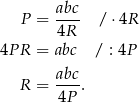
W podobny sposób wyznaczmy  .
.
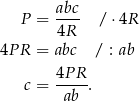
Odpowiedź: A, D

