Zadanie nr 8320121
Ula i Kajtek mają razem 22 lata. Pięć lat temu Ula była 3 razy starsza od Kajtka.
Ile lat temu Ula była dwa razy starsza od Kajtka?
A) 1 B) 2 C) 3 D) 4
Rozwiązanie
Sposób I
Pięć lat temu Ula i Kajtek mieli razem 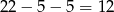 lat. Ula była wtedy 3 razy starsza od Kajtka, więc miała 9 lat, a Kajtek miał 3 lata. To oznacza, że mają teraz odpowiednio 14 i 8 lat. W takim razie Ula była dwa razy starsza od Kajtka dwa lata temu, gdy mieli odpowiednio 12 i 6 lat.
lat. Ula była wtedy 3 razy starsza od Kajtka, więc miała 9 lat, a Kajtek miał 3 lata. To oznacza, że mają teraz odpowiednio 14 i 8 lat. W takim razie Ula była dwa razy starsza od Kajtka dwa lata temu, gdy mieli odpowiednio 12 i 6 lat.
Sposób II
Oznaczmy wiek Uli przez  , a wiek Kajtka przez
, a wiek Kajtka przez 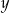 . Zatem
. Zatem 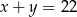 oraz
oraz
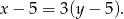
Podstawmy w tej równości 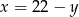 .
.
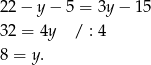
Stąd 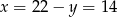 . To oznacza, że Ula i Kajtek mają teraz odpowiednio 14 i 8 lat. Ula była dwa razy starsza od Kajtka dwa lata temu, gdy mieli odpowiednio 12 i 6 lat.
. To oznacza, że Ula i Kajtek mają teraz odpowiednio 14 i 8 lat. Ula była dwa razy starsza od Kajtka dwa lata temu, gdy mieli odpowiednio 12 i 6 lat.
Odpowiedź: B

