Zadanie nr 8382601
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli długość każdej krawędzi podstawy ostrosłupa prawidłowego czworokątnego zwiększymy 2 razy, a jego wysokość zmniejszymy 2 razy, to objętość ostrosłupa
A) zwiększy się czterokrotnie. B) zwiększy się dwukrotnie.
C) zmniejszy się dwukrotnie. D) nie zmieni się.
Rozwiązanie
Naszkicujmy ostrosłup prawidłowy czworokątny.
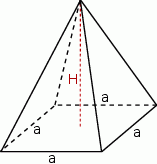
Jeżeli krawędź podstawy ostrosłupa prawidłowego czworokątnego jest równa  , a wysokość jest równa
, a wysokość jest równa 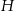 to jego objętość jest równa
to jego objętość jest równa
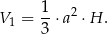
Po opisanych zmianach otrzymamy ostrosłup z krawędzią podstawy długości 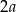 i wysokością
i wysokością 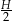 . Jego objętość jest równa
. Jego objętość jest równa
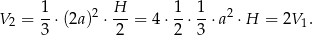
Objętość zwiększyła się więc 2 razy.
Odpowiedź: B

