/Szkoła podstawowa/Zadania testowe

Zadanie nr 8974270

Dodaj do ulubionych
Dodaj do rozwiązanych

Cenę telewizora obniżono o 15%, a następnie o 2%. Klient kupił telewizor po obniżonej cenie i dzięki temu zapłacił o 501 zł mniej, niż zapłaciłby przed obniżkami. Przed obniżkami ten telewizor kosztował
A) 2947 zł B) 4000 zł C) 3000 zł D) 2840 zł

Rozwiązanie

Niech x oznacza cenę telewizora przed obniżkami.

Sposób I

Po pierwszej obniżce telewizor kosztował

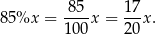
85 1 7 85%x = ----x = ---x. 100 2 0

Po drugiej obniżce telewizor kosztował

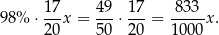
17 49 1 7 833 98% ⋅--x = ---⋅--- = -----x. 20 50 2 0 1 000

W takim razie cenę obniżono o

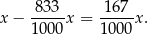
-833- 167-- x− 1000 x = 1000x .

Stąd

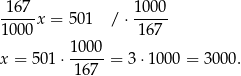
167-x = 501 / ⋅ 1000- 1000 16 7 1000 x = 501 ⋅-----= 3 ⋅1000 = 3 000. 167

Sposób II

Po obniżkach telewizor kosztował

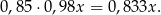
0,85 ⋅0,98x = 0,833x.

Mamy zatem

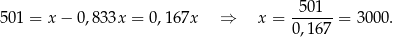
-501-- 501 = x − 0 ,833x = 0 ,167x ⇒ x = 0,167 = 3000 .

 
Odpowiedź: C

Wersja PDF