Zadanie nr 9180558
Punkt 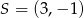 jest środkiem odcinka
jest środkiem odcinka 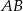 i
i 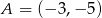 . Punkt
. Punkt 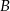 ma współrzędne
ma współrzędne
A) 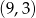 B)
B) 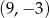 C)
C) 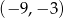 D)
D) 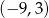
Rozwiązanie
Sposób I
Korzystamy ze wzoru
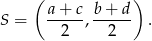
na środek odcinka o końcach 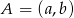 i
i 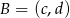 . Mamy więc równanie
. Mamy więc równanie
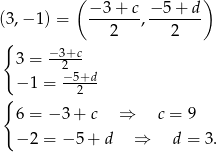
Zatem 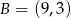
Sposób II
Jak poprzednio korzystamy ze wzoru na środek odcinka, ale tym razem sprawdzamy podane odpowiedzi.
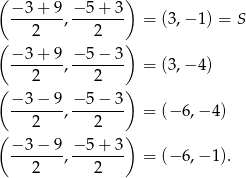
Widzimy zatem, że poprawną odpowiedzią jest 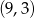 .
.
Sposób III
Wykonujemy w miarę dokładny rysunek i zgadujemy o jaki punkt chodzi.
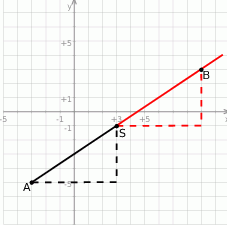
Zaznaczamy najpierw punkty 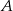 i
i 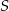 , rysujemy odcinek łączący je, a następnie rysujemy trójkąt prostokątny (czarna przerywana linia). Przedłużamy odcinek
, rysujemy odcinek łączący je, a następnie rysujemy trójkąt prostokątny (czarna przerywana linia). Przedłużamy odcinek 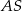 (czerwona linia) i rysujemy czerwony trójkąt prostokątny, który jest przystający do czarnego trójkąta. Otrzymamy w ten sposób szukany punkt
(czerwona linia) i rysujemy czerwony trójkąt prostokątny, który jest przystający do czarnego trójkąta. Otrzymamy w ten sposób szukany punkt 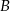 . Można odczytać z obrazka, że
. Można odczytać z obrazka, że 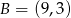 .
.
Odpowiedź: A

