/Szkoła podstawowa/Zadania testowe

Zadanie nr 9638083

Dodaj do ulubionych
Dodaj do rozwiązanych

Jacek wyciął z kartki papieru dwa jednakowe trójkąty prostokątne o bokach długości 18 cm, 24 cm i 30 cm. Pierwszy z nich zagiął wzdłuż symetralnej dłuższej przyprostokątnej, a drugi – wzdłuż symetralnej krótszej przyprostokątnej. W ten sposób otrzymał czworokąty pokazane na rysunkach.

PIC

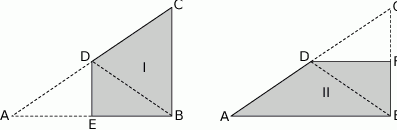
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.

Pole czworokąta I jest równe polu czworokąta II. PF
Obwód czworokąta I jest mniejszy od obwodu czworokąta II.PF

Rozwiązanie

Zauważmy, że pierwszym przypadku zagięty (biały) trójkąt ma pole równe

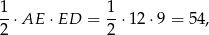
1-⋅AE ⋅ ED = 1-⋅1 2⋅9 = 54, 2 2

a w drugim przypadku to pole jest równe

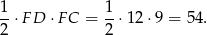
1 1 --⋅FD ⋅FC = --⋅12 ⋅9 = 5 4. 2 2

To oznacza, że pola otrzymanych czworokątów są takie same (bo w obu przypadkach startujemy od tego samego trójkąta 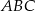ABC ). Obwody czworokątów są odpowiednio równe

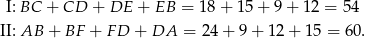
I: BC + CD + DE + EB = 18 + 15 + 9 + 12 = 54 II: AB + BF + F D + DA = 24+ 9+ 12+ 15 = 60.

 
Odpowiedź: P, P

Wersja PDF