Zadanie nr 8980196
Do pojemnika wsypano 200 koralików białych i 300 czerwonych. Wymieszano je i zapakowano do woreczków po 50 sztuk. Okazało się, że w jednym z woreczków znalazły się tylko białe koraliki.
Wobec tego nie jest możliwe, aby
A) wszystkie pozostałe białe koraliki znajdowały się w trzech woreczkach.
B) w jednym z pozostałych woreczków nie było białych koralików.
C) w większości pozostałych woreczków znalazło się po 17 białych koralików.
D) w każdym z pozostałych woreczków było więcej koralików białych niż czerwonych.
Rozwiązanie
Zauważmy najpierw, że wszystkich woreczków było
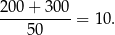
Skoro w wybranym woreczku jest 50 białych koralików, to w pozostałych woreczkach jest 150 białych i oczywiście mogą być wszystkie w trzech woreczkach.
Tym samym niektóre z woreczków mogą nie zawierać białych koralików.
Jak zauważyliśmy pozostało 9 woreczków, jeżeli w 5 z nich jest 17 koralików to nadal pozostaje
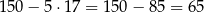
białych koralików. Nie ma przeszkód, aby rozmieścić je w pozostałych 4 woreczkach.
Gdyby w każdym pozostałym woreczku było więcej koralików białych niż czerwonych, to w sumie byłoby więcej koralików białych niż czerwonych, a to jak wiemy nie jest prawdą.
Odpowiedź: D

