Zadanie nr 9062894
Ile jest wszystkich czterocyfrowych liczb naturalnych mniejszych niż 2017?
A) 2016 B) 2017 C) 1016 D) 1017
Rozwiązanie
Sposób I
Wszystkich liczb naturalnych mniejszych od 2017 jest 2016:
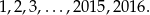
Wśród nich jest 999 liczb, które nie są czterocyfrowe:
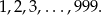
W takim razie jest
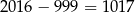
liczb czterocyfrowych mniejszych od 2017.
Sposób II
Liczb czterocyfrowych rozpoczynających się od jedynki (czyli mniejszych od 2000) jest
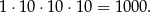
Do tego jest 17 liczb pomiędzy 1999 i 2017. W sumie jest więc
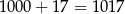
liczb spełniających warunki zadania.
Odpowiedź: D

