Zadanie nr 1843668
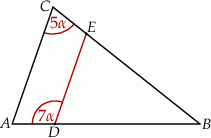
Odcinek 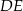 jest równoległy do podstawy
jest równoległy do podstawy 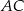 trójkąta równoramiennego
trójkąta równoramiennego 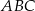 (zobacz rysunek).
(zobacz rysunek).
Kąt 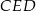 ma miarę A/B.
ma miarę A/B.
A) 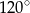 B)
B) 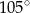
Kąt 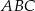 ma miarę C/D.
ma miarę C/D.
C) 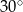 D)
D) 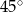
Rozwiązanie
Trójkąt 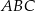 jest równoramienny, więc
jest równoramienny, więc
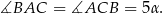
Proste 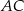 i
i 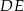 są równoległe, więc
są równoległe, więc
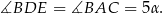
Mamy zatem
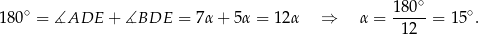
Stąd
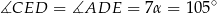
i
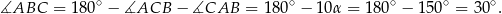
Odpowiedź: B, C

