Zadanie nr 2594542
Wykonano następującą konstrukcję.
1. Narysowano trójkąt 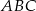 . 2. Wykreślono dwusieczne dwóch kątów wewnętrznych tego trójkąta i ich punkt przecięcia oznaczono literą
. 2. Wykreślono dwusieczne dwóch kątów wewnętrznych tego trójkąta i ich punkt przecięcia oznaczono literą 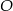 .
.
3. Poprowadzono prostą prostopadłą do boku 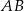 i przechodzącą przez punkt
i przechodzącą przez punkt 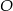 . Punkt przecięcia tej prostej i boku
. Punkt przecięcia tej prostej i boku 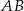 oznaczono literą
oznaczono literą 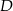 .
.
4. Narysowano okrąg o środku w punkcie 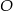 i promieniu
i promieniu 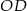 .
.
Skonstruowany w opisany powyżej sposób okrąg
A) przechodzi przez wszystkie wierzchołki tego trójkąta.
B) jest styczny do wszystkich boków tego trójkąta.
C) ma środek leżący na jednym z boków trójkąta.
D) przecina jeden z boków trójkąta w dwóch punktach.
Rozwiązanie
Szkicujemy opisaną konstrukcję
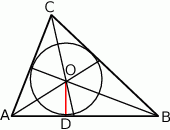
Widać, że skonstruowaliśmy okrąg wpisany w trójkąt.
Odpowiedź: B

