/Szkoła podstawowa/Zadania testowe/Geometria/Trójkąty

Zadanie nr 2750449

Jeżeli 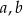a,b i c są długościami boków trójkąta oraz c jest najdłuższym bokiem, to ten trójkąt jest:
 – prostokątny, gdy 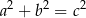a2 + b2 = c2
 – rozwartokątny, gdy 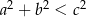a2 + b2 < c2
 – ostrokątny, gdy 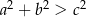2 2 2 a + b > c .
Z odcinków o długościach: 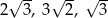√ -- √ -- √ -- 2 3 , 3 2, 3
A) nie można zbudować trójkąta. B) można zbudować trójkąt prostokątny.
C) można zbudować trójkąt rozwartokątny. D) można zbudować trójkąt ostrokątny.

Wersja PDF

Rozwiązanie

Sprawdźmy najpierw, czy z danych odcinków można zbudować trójkąt – w tym celu musimy sprawdzić, czy najdłuższy z nich jest krótszy od sumy dwóch pozostałych. Tak jednak jest, bo

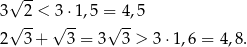
√ -- 3 2 < 3 ⋅1,5 = 4,5 √ -- √ -- √ -- 2 3 + 3 = 3 3 > 3 ⋅1,6 = 4,8.

Ponieważ

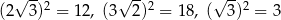
√ -- √ -- √ -- (2 3)2 = 12, (3 2)2 = 18, ( 3)2 = 3

i 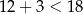12 + 3 < 18 z podanych odcinków o podanych długościach można zbudować trójkąt rozwartokątny.  
Odpowiedź: C

Wersja PDF