Zadanie nr 2963247
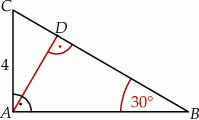
Odcinek 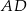 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 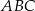 , w którym przyprostokątna
, w którym przyprostokątna 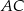 ma długość 4 cm i kąt ostry
ma długość 4 cm i kąt ostry 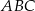 ma miarę
ma miarę 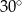 (zobacz rysunek).
(zobacz rysunek).
Kąt 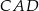 ma miarę A/B.
ma miarę A/B.
A) 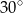 B)
B) 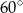
Odcinek 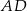 ma długość C/D.
ma długość C/D.
C) 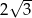 D)
D) 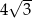
Rozwiązanie
Zauważmy, że
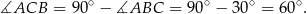
Stąd
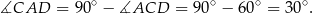
Długość odcinka 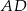 obliczymy na dwa sposoby.
obliczymy na dwa sposoby.
Sposób I
Trójkąt prostokątny 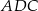 jest połówką trójkąta równobocznego o boku długości
jest połówką trójkąta równobocznego o boku długości 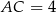 . Zatem
. Zatem 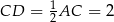 i
i
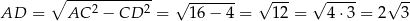
(mogliśmy też skorzystać z gotowego wzoru 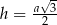 na wysokość w trójkącie równobocznym o boku
na wysokość w trójkącie równobocznym o boku  ).
).
Sposób II
Narysowany trójkąt 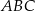 jest połówką trójkąta równobocznego o boku długości
jest połówką trójkąta równobocznego o boku długości 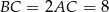 . Odcinek
. Odcinek 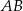 ma więc długość
ma więc długość
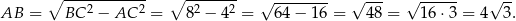
Możemy teraz na dwa sposoby obliczyć pole trójkąta 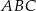
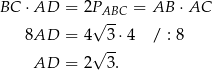
Odpowiedź: A, C

