Zadanie nr 6301832
Na bokach trójkąta prostokątnego 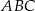 zaznaczono punkty
zaznaczono punkty 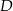 i
i 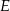 . Odcinek
. Odcinek 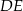 podzielił trójkąt
podzielił trójkąt 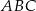 na dwa wielokąty: trójkąt prostokątny
na dwa wielokąty: trójkąt prostokątny 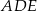 i czworokąt
i czworokąt 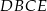 , jak na rysunku. Odcinek
, jak na rysunku. Odcinek 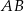 ma długość
ma długość 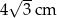 , a odcinek
, a odcinek 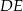 ma długość 3 cm.
ma długość 3 cm.
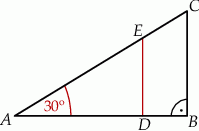
Długość odcinka 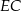 jest równa
jest równa
A) 1 cm B) 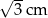 C) 2 cm D) 4 cm E)
C) 2 cm D) 4 cm E) 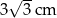
Rozwiązanie
Zauważmy, że każdy z trójkątów 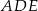 i
i 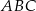 to połówka trójkąt równobocznego. W szczególności
to połówka trójkąt równobocznego. W szczególności
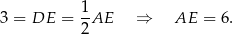
W trójkącie 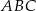 znamy długość wysokości
znamy długość wysokości 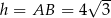 , co pozwala nam obliczyć długość jego boku
, co pozwala nam obliczyć długość jego boku
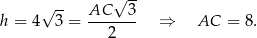
Stąd
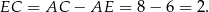
Odpowiedź: C

