Zadanie nr 6731630
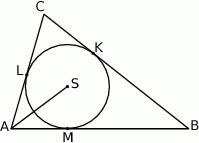
Punkt 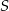 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 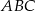 , a punkty
, a punkty 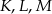 są punktami styczności tego okręgu z bokami trójkąta. Odcinek
są punktami styczności tego okręgu z bokami trójkąta. Odcinek 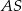 ma długość 26 cm, a odcinek
ma długość 26 cm, a odcinek 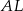 ma długość 24 cm.
ma długość 24 cm.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Promień okręgu wpisanego w trójkąt 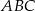 jest równy 9 cm. jest równy 9 cm. | P | F |
Odcinki 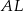 i i 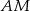 mają tę samą długość. mają tę samą długość. | P | F |
Rozwiązanie
Dorysujmy promienie okręgu wpisanego.
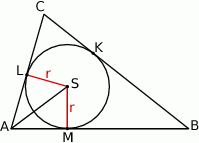
Trójkąty 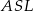 i
i 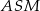 są prostokątne, bo styczna do okręgu jest zawsze prostopadła do promienia łączącego środek okręgu z punktem styczności. Ponadto trójkąty te mają dwa boki tej samej długości:
są prostokątne, bo styczna do okręgu jest zawsze prostopadła do promienia łączącego środek okręgu z punktem styczności. Ponadto trójkąty te mają dwa boki tej samej długości: 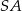 i
i 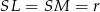 . To oznacza, że trójkąty te są przystające, więc
. To oznacza, że trójkąty te są przystające, więc 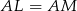 .
.
Promień okręgu wpisanego w trójkąt obliczamy z twierdzenia Pitagorasa w trójkącie 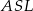 .
.
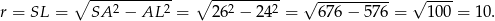
Odpowiedź: F, P

