/Szkoła podstawowa/Zadania testowe/Geometria/Trójkąty

Zadanie nr 8084689

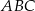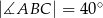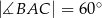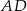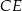W trójkącie ABC , w którym ∘ |∡ABC | = 40 , ∘ |∡BAC | = 60 poprowadzono dwusieczne AD i CE , które przecinają się w punkcie F .

PIC

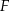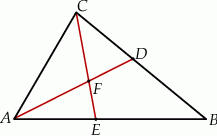
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.

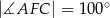|∡AF C| = 10 0∘ PF
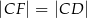|CF | = |CD | PF
Wersja PDF

Rozwiązanie

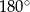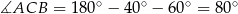Suma kątów w trójkącie wynosi ∘ 180 , więc ∘ ∘ ∘ ∘ ∡ACB = 180 − 40 − 60 = 8 0 .

PIC

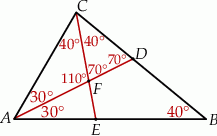
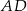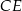Ponieważ AD i CE są dwusiecznymi, mamy ponadto

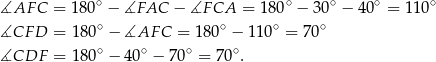
∘ ∘ ∘ ∘ ∘ ∡AF C = 180 − ∡FAC − ∡F CA = 180 − 30 − 40 = 110 ∡CF D = 180∘ − ∡AF C = 180∘ − 110∘ = 70∘ ∘ ∘ ∘ ∘ ∡CDF = 180 − 40 − 70 = 70 .

W takim razie trójkąt 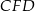CF D jest równoramienny i CF = CD .  
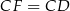Odpowiedź: F, P

Wersja PDF