/Szkoła podstawowa/Zadania testowe/Figury przestrzenne

Zadanie nr 3779929

Dodaj do ulubionych
Dodaj do rozwiązanych

Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego czworokątnego.

PIC

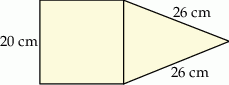
Suma długości krawędzi bocznych tego ostrosłupa jest równa A/B.
A) 360 cm B) 104 cm
Pole powierzchni całkowitej tego ostrosłupa jest równa C/D.
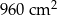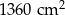
C) 2 960 cm D) 2 1 360 cm

Rozwiązanie

Wszystkie krawędzie boczne ostrosłupa mają oczywiście długość 26 cm, więc ich suma jest równa

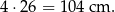
4 ⋅26 = 10 4 cm .

PIC

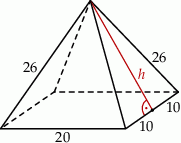
Wysokość ściany bocznej ma długość

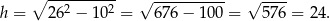
∘ ---------- √ ---------- √ ---- h = 262 − 102 = 6 76− 100 = 57 6 = 24.

Pole powierzchni całkowitej jest więc równe

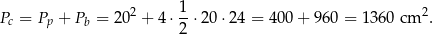
Pc = Pp + Pb = 202 + 4 ⋅ 1-⋅20 ⋅24 = 40 0+ 960 = 136 0 cm 2. 2

 
Odpowiedź: B, D

Wersja PDF