/Szkoła podstawowa/Zadania testowe/Geometria/Różne

Zadanie nr 4896531

Dodaj do ulubionych
Dodaj do rozwiązanych

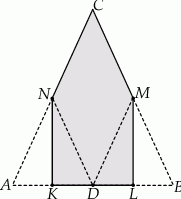
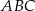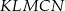Łukasz wyciął z kartki papieru trójkąt równoramienny ABC , a następnie zagiął w nim dwa narożniki tak, że wierzchołki A i B trójkąta znalazły się w środku D jego podstawy. Powstał w ten sposób pięciokąt KLMCN .

PIC

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.

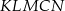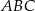Pole pięciokąta KLMCN stanowi 75% pola trójkąta ABC . PF
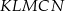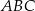Obwód pięciokąta KLMCN jest taki sam jak obwód trójkąta ABC .PF

Rozwiązanie

Aby obliczyć pole pięciokąta 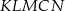KLMCN zauważmy, że powstał on z trójkąta 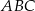ABC poprzez odcięcie dwóch przystających trójkątów prostokątnych 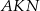AKN . Każdy z tych trójkątów jest podobny do trójkąta 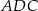ADC w skali 1:2, więc pole każdego z nich jest równe

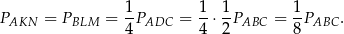
1- 1- 1- 1- PAKN = PBLM = 4PADC = 4 ⋅ 2PABC = 8PABC .

W takim razie pole pięciokąta 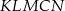KLMCN jest równe

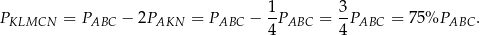
P = P − 2P = P − 1P = 3P = 75 %P . KLMCN ABC AKN ABC 4 ABC 4 ABC ABC

Jeżeli chodzi natomiast o obwód pięciokąta 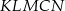KLMCN , to jest on wyraźnie mniejszy od obwodu trójkąta ABC .

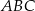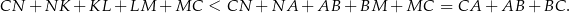
CN + NK + KL + LM + MC < CN + NA + AB + BM + MC = CA + AB + BC .

 
Odpowiedź: P, F

Wersja PDF