/Szkoła podstawowa/Zadania testowe/Geometria/Różne

Zadanie nr 8514172

Dodaj do ulubionych
Dodaj do rozwiązanych

Dwie przecinające się proste utworzyły cztery kąty. Suma miar trzech z tych kątów jest równa 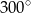300∘ . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.

Suma miar kątów ostrych wyznaczonych przez te proste jest równa 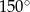∘ 150 .PF
Jeden z dwóch kątów przyległych jest dwa razy większy od drugiego kąta.PF

Rozwiązanie

Szkicujemy dwie przecinające się proste.

PIC

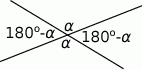
Dany warunek możemy zapisać w postaci

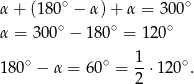
∘ ∘ α+ (180 − α) + α = 300 α = 300 ∘ − 1 80∘ = 120 ∘ 180∘ − α = 6 0∘ = 1-⋅120 ∘. 2

W takim razie suma kątów ostrych wyznaczonych przez te proste jest równa 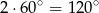2 ⋅60∘ = 1 20∘ oraz jeden z kątów przyległych jest dwa razy większy od drugiego.  
Odpowiedź: F, P

Wersja PDF