Zadanie nr 5295657
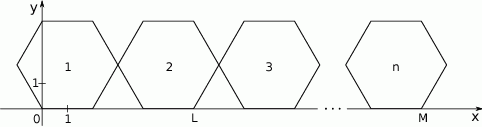
W układzie współrzędnych narysowano sześciokąt foremny o boku 2 tak, że jednym z jego wierzchołków jest punkt 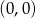 , a jeden z jego boków leży na osi
, a jeden z jego boków leży na osi  . Do tego sześciokąta dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi
. Do tego sześciokąta dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi  . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwsza współrzędna wierzchołka 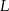 w drugim sześciokącie jest równa 6. w drugim sześciokącie jest równa 6. | P | F |
Pierwsza współrzędna wierzchołka 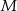 w w  –tym sześciokącie jest równa –tym sześciokącie jest równa 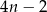 . . | P | F |
Rozwiązanie
Jeżeli połączymy wierzchołki sześciokąta foremnego z jego środkiem, to otrzymujemy 6 trójkątów równobocznych.
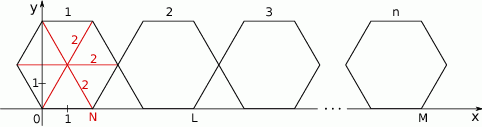
W takim razie szerokość każdego z sześciokątów jest równa 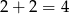 , a wierzchołek
, a wierzchołek 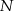 na rysunku ma współrzędne
na rysunku ma współrzędne 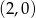 . Wierzchołek
. Wierzchołek  otrzymujemy przesuwając
otrzymujemy przesuwając 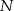 o szerokość sześciokąta, więc
o szerokość sześciokąta, więc 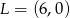 .
.
Dokładnie w ten sposób wyznaczamy współrzędne wierzchołka 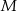 – aby otrzymać ten punkt musimy przesunąć
– aby otrzymać ten punkt musimy przesunąć 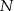 o
o 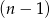 szerokości sześciokąta. Stąd
szerokości sześciokąta. Stąd
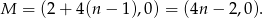
Odpowiedź: P, P

