/Szkoła podstawowa/Zadania testowe/Geometria/Układ współrzędnych

Zadanie nr 7291065

Dodaj do ulubionych
Dodaj do rozwiązanych

Na kwadratowej siatce narysowano pewien wielokąt (patrz rysunek). Jego wierzchołki znajdują się w punktach przecięcia linii siatki.

PIC

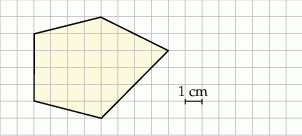
Pole tego wielokąta jest równe
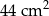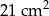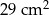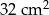
A) 44 cm 2 B) 21 cm 2 C) 29 cm 2 D) 32 cm 2

Rozwiązanie

Sposób I

Pole narysowanego czworokąta możemy obliczyć odejmując od pola prostokąta o bokach długości 8 cm i 6 cm pola czterech trójkątów prostokątnych.

PIC

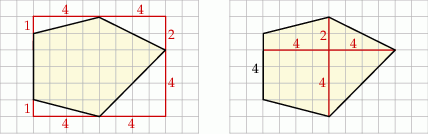
Jest więc ono równe

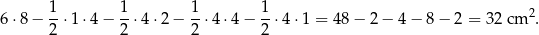
1 1 1 1 6⋅ 8− -⋅ 1⋅4 − --⋅4 ⋅2 − --⋅4 ⋅4− --⋅4⋅1 = 48− 2− 4− 8 − 2 = 32 cm 2. 2 2 2 2

Sposób II

Pole czworokąta możemy też obliczyć jako sumę pola trapezu o podstawach 4, 6 i wysokości 4 oraz trójkąta o podstawie 6 i wysokości 4. Pole jest więc równe

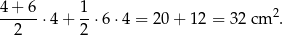
4+ 6 1 -----⋅4 + -⋅ 6⋅4 = 20+ 12 = 32 cm 2. 2 2

 
Odpowiedź: D

Wersja PDF