Zadanie nr 9306671
Na rysunkach zaznaczono cztery wielokąty o wierzchołkach w punktach przecięcia się linii siatki. Wskaż wielokąt, którego pole jest inne niż pola trzech pozostałych wielokątów.
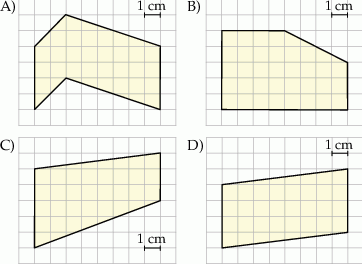
Rozwiązanie
Pole wielokąta na rysunku A jest takie samo jak pole prostokąta o bokach długości 4 cm i 8 cm, czyli jest równe 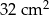 .
.
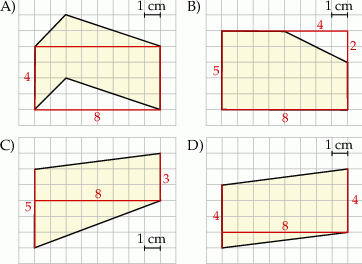
Na rysunku C mamy trapez o podstawach długości 5 cm i 3 cm oraz wysokości 8 cm. Jego pole jest równe
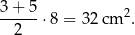
Na rysunku D jest równoległobok o podstawie długości 4 cm i wysokości 8 cm. Jego pole też jest równe 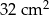 .
.
Natomiast wielokąt z rysunku B ma większe pole – możemy je obliczyć odejmując od pola prostokąta o bokach 8 cm i 5 cm pole trójkąta prostokątnego o przyprostokątnych długości 2 cm i 4 cm. Pole to jest więc równe
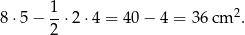
Odpowiedź: B

