Zadanie nr 2931317
W dodatniej liczbie trzycyfrowej cyfra dziesiątek jest średnią arytmetyczną jej pozostałych dwóch cyfr, a iloczyn cyfr setek i jedności jest równy 12. Ile jest liczb spełniających te warunki?
A) Jedna. B) Dwie. C) Trzy. D) Cztery.
Rozwiązanie
Zastanówmy się najpierw jakie mogą być cyfry setek i jedności tej liczby. Ich iloczyn ma być równy 12, więc mogą to być
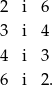
Zauważmy jednak, że suma cyfr jedności i setek musi być parzysta tak, aby cyfra dziesiątek mogła być ich średnią. Są więc tylko 2 możliwości: 256 i 652.
Odpowiedź: B

