Zadanie nr 6653718
Rozważmy treść następującego zadania:
Obwód rombu o przekątnych długości  i
i 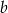 jest równy 48. Pole tego rombu jest równe 16. Oblicz długości przekątnych tego rombu.
jest równy 48. Pole tego rombu jest równe 16. Oblicz długości przekątnych tego rombu.
Który układ równań opisuje zależności między długościami przekątnych tego rombu?
A) 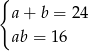 B)
B) 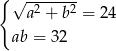 C)
C) 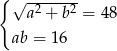 D)
D) 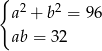
Rozwiązanie
Szkicujemy romb.
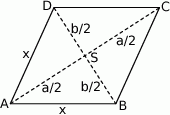
Jeżeli oznaczymy przez 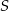 środek rombu, a przez
środek rombu, a przez  długość jego boku, to z trójkąta prostokątnego
długość jego boku, to z trójkąta prostokątnego 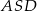 mamy
mamy
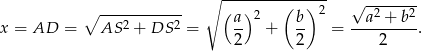
Obwód rombu jest więc równy
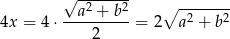
i podana informacja o obwodzie prowadzi do równania
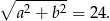
Aby zapisać informację o polu rombu korzystamy ze wzoru na pole z przekątnymi.
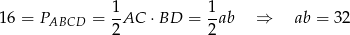
Odpowiedź: B

