Zadanie nr 8556998
Dany jest układ równań
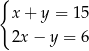
Liczby  i
i 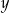 spełniające ten układ równań spełniają też warunek:
spełniające ten układ równań spełniają też warunek:
A)  i
i 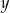 są liczbami parzystymi. B)
są liczbami parzystymi. B)  i
i 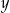 są liczbami ujemnymi.
są liczbami ujemnymi.
C) suma  i
i 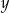 jest podzielna przez 3. D) różnica
jest podzielna przez 3. D) różnica  i
i 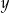 jest równa 0.
jest równa 0.
Rozwiązanie
Sposób I
Dodajmy do pierwszego równania drugie (żeby skrócić 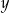 ). Mamy wtedy
). Mamy wtedy
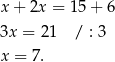
Stąd 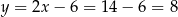 .
.
Liczby 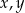 nie są obie parzyste, nie są też ujemne. Ich różnica nie jest równa 0. Natomiast suma
nie są obie parzyste, nie są też ujemne. Ich różnica nie jest równa 0. Natomiast suma
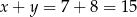
dzieli się przez 3.
Sposób II
Zauważmy, że pierwsze równanie układu oznacza, że suma liczb  i
i 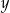 dzieli się przez 3. Wiemy, że jest tylko jedna prawidłowa odpowiedź, więc pozostałych odpowiedzi możemy nie sprawdzać.
dzieli się przez 3. Wiemy, że jest tylko jedna prawidłowa odpowiedź, więc pozostałych odpowiedzi możemy nie sprawdzać.
Odpowiedź: C

