Zadanie nr 4603670
Podstawą ostrosłupa jest romb o boku długości 18 cm. Każda ze ścian bocznych tworzy z płaszczyzną podstawy kąt 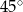 . Pole powierzchni bocznej ostrosłupa jest równe
. Pole powierzchni bocznej ostrosłupa jest równe 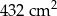 . Oblicz jego objętość.
. Oblicz jego objętość.
Rozwiązanie
Oczywiście zaczynamy od dużego rysunku.
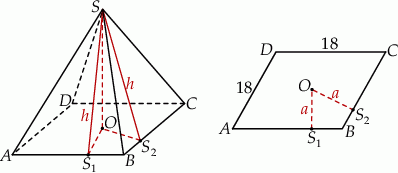
Najtrudniejsze w tym zadaniu jest ustalenie, jaki jest prawdziwy kształt opisanej bryły. Jest to o tyle trudne, że rysując rzuty ostrosłupów prawidłowych i tak rysujemy w podstawie romb, więc bardzo trudno jest odróżnić naszą obecną sytuację od dobrze nam znanej sytuacji ostrosłupa prawidłowego. Podstawowe dwa pytania, na które musimy sobie odpowiedzieć to: gdzie jest spodek wysokości ostrosłupa? – czy musi to być środek rombu? Drugie pytanie, to co można powiedzieć o ścianach bocznych ostrosłupa? – np. czy muszą być przystające?
Co mamy dane? – pole powierzchni bocznej – to nam nic nie mówi o kształcie, tylko o wielkości. Druga dana, to informacja o kątach nachylenia ścian bocznych i to jest to co musimy wykorzystać.
Spróbujmy wyobrazić sobie jak skonstruować opisaną figurę – bierzemy romb i przez każdą jego krawędź prowadzimy płaszczyznę nachyloną do płaszczyzny rombu pod kątem 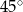 . Żeby lepiej widzieć co się dzieje (chcemy ustalić gdzie jest wierzchołek ostrosłupa), najpierw poprowadźmy dwie płaszczyzny przez dwa równoległe boki rombu. Płaszczyzny te przetną się wzdłuż prostej, której rzut na płaszczyznę rombu będzie równo odległy od dwóch równoległych boków rombu, od których zaczęliśmy (bo płaszczyzny są nachylone pod tym samym kątem!). Wierzchołek ostrosłupa leży na tej prostej, więc jego rzut też jest w tej samej odległości od dwóch równoległych boków rombu. Podobnie uzasadniamy, że ten rzut jest równo odległy od dwóch pozostałych boków, jest to więc środek rombu.
. Żeby lepiej widzieć co się dzieje (chcemy ustalić gdzie jest wierzchołek ostrosłupa), najpierw poprowadźmy dwie płaszczyzny przez dwa równoległe boki rombu. Płaszczyzny te przetną się wzdłuż prostej, której rzut na płaszczyznę rombu będzie równo odległy od dwóch równoległych boków rombu, od których zaczęliśmy (bo płaszczyzny są nachylone pod tym samym kątem!). Wierzchołek ostrosłupa leży na tej prostej, więc jego rzut też jest w tej samej odległości od dwóch równoległych boków rombu. Podobnie uzasadniamy, że ten rzut jest równo odległy od dwóch pozostałych boków, jest to więc środek rombu.
Jeżeli ktoś się w tym wywodzie pogubił, to można sobie też myśleć następująco. Jeżeli weźmiemy płaszczyznę równoległą do odcinków 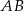 i
i 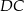 i przechodzącą przez wysokość
i przechodzącą przez wysokość 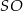 , to tworzy ona jednakowe kąty
, to tworzy ona jednakowe kąty 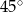 z płaszczyznami
z płaszczyznami 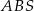 i
i 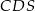 . Zatem symetria względem tej płaszczyzny zamienia płaszczyzny
. Zatem symetria względem tej płaszczyzny zamienia płaszczyzny 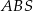 i
i 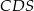 ze sobą. Ponadto symetria ta przeprowadza płaszczyznę
ze sobą. Ponadto symetria ta przeprowadza płaszczyznę 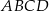 na siebie, zatem prosta
na siebie, zatem prosta 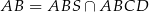 musi przejść na prostą
musi przejść na prostą 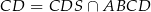 . To oznacza, że wysokość
. To oznacza, że wysokość 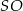 jest dokładnie w połowie między prostymi
jest dokładnie w połowie między prostymi 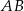 i
i 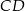 .
.
Jeszcze inne, najprostsze uzasadnienie, to jak przetniemy ostrosłup płaszczyzną prostopadłą do krawędzi podstawy i przechodzącą przez wysokość 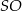 (płaszczyzna
(płaszczyzna 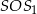 na rysunku) to otrzymamy trójkąt z dwoma równymi kątami, a więc równoramienny (na rysunku jest tylko połowa tego trójkąta). Zatem jego wysokość opuszczona na podstawę dzieli podstawę trójkąta na połowy.
na rysunku) to otrzymamy trójkąt z dwoma równymi kątami, a więc równoramienny (na rysunku jest tylko połowa tego trójkąta). Zatem jego wysokość opuszczona na podstawę dzieli podstawę trójkąta na połowy.
Ok, jeżeli już uwierzymy, że spodek wysokości to środek rombu, to dalej jest łatwo, np. jest teraz jasne, że ściany są przystające (bo 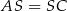 i
i 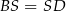 ).
).
Niech 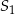 i
i 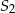 będą rzutami punktu
będą rzutami punktu 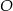 na krawędzie
na krawędzie 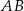 i
i 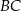 . W szczególności
. W szczególności 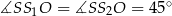 . Ponieważ
. Ponieważ 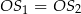 (połowa wysokości rombu), to
(połowa wysokości rombu), to 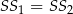 . Jeżeli oznaczymy długości tych odcinków przez
. Jeżeli oznaczymy długości tych odcinków przez  i
i 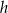 , to z trójkąta
, to z trójkąta 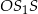 mamy
mamy 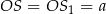 i
i 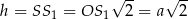 . Popatrzmy teraz co mamy dane.
. Popatrzmy teraz co mamy dane.
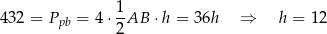
Mamy obliczyć objętość
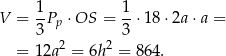
Odpowiedź: