Zadanie nr 1038376
Najmniejszym rozwiązaniem równania 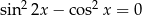 w przedziale
w przedziale 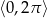 jest liczba
jest liczba
A) 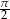 B)
B) 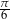 C)
C) 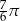 D)
D) 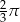
Rozwiązanie
Przekształćmy dane równanie
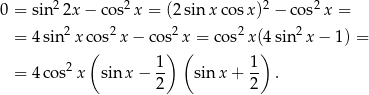
Zatem
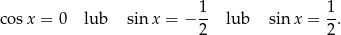
Szkicujemy teraz sinusa i cosinusa.
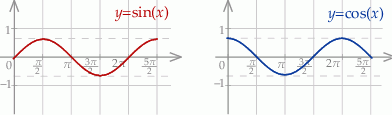
Z wykresów powinno być jasne, że najmniejszą liczbą spełniającą to równanie jest
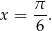
Odpowiedź: B

