/Szkoła średnia/Geometria/Planimetria/Czworokąt/Prostokąt/Udowodnij

Zadanie nr 1265487

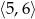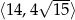Dany jest prostokąt o polu 12, w którym długość przekątnej jest liczbą z przedziału ⟨5,6⟩ . Wykaż, że obwód tego prostokąta jest liczbą z przedziału √ --- ⟨14 ,4 15⟩ .

Wersja PDF

Rozwiązanie

Szkicujemy prostokąt.

PIC

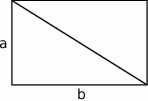
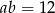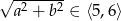Wiemy, że ab = 12 oraz √ ------- a2 + b2 ∈ ⟨5,6⟩ . Przekształcamy daną nierówność na długość przekątnej tak, aby oszacować a + b .

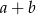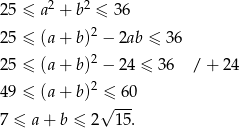
25 ≤ a2 + b2 ≤ 36 2 25 ≤ (a + b) − 2ab ≤ 36 25 ≤ (a + b)2 − 24 ≤ 36 / + 24 2 49 ≤ (a + b) ≤ 60 √ --- 7 ≤ a+ b ≤ 2 15 .

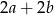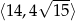Zatem obwód prostokąta 2a+ 2b musi być liczbą z przedziału √ --- ⟨14 ,4 15⟩ .

Wersja PDF