Zadanie nr 1503800
Punkt 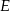 jest środkiem boku
jest środkiem boku 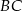 prostokąta
prostokąta 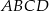 , w którym
, w którym 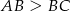 . Punkt
. Punkt 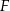 leży na boku
leży na boku 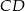 tego prostokąta oraz
tego prostokąta oraz 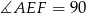 . Udowodnij, że
. Udowodnij, że 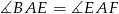 .
.
Rozwiązanie
Sposób I
Niech 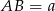 i
i 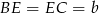 .
.
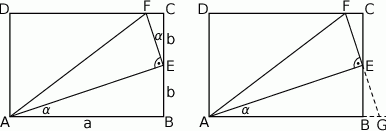
Zauważmy, że oba trójkąty 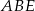 i
i 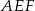 są prostokątne, więc jest dość łatwo obliczyć np. tangensy interesujących nas kątów. Z pierwszego z tych trójkątów mamy
są prostokątne, więc jest dość łatwo obliczyć np. tangensy interesujących nas kątów. Z pierwszego z tych trójkątów mamy
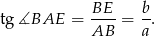
Zanim obliczymy tangens drugiego z interesujących nas kątów, zauważmy, że trójkąty prostokątne 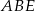 i
i 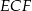 mają równe kąty ostre (bo
mają równe kąty ostre (bo 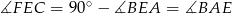 ), więc są podobne. W takim razie
), więc są podobne. W takim razie
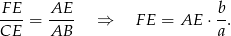
W takim razie
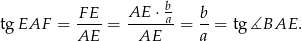
To oznacza, że rzeczywiście 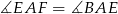 .
.
Sposób II
Tak jak w poprzednim sposobie oznaczmy 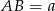 i
i 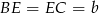 . Trójkąty
. Trójkąty 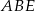 i
i 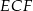 są prostokątne i mają równe kąty ostre
są prostokątne i mają równe kąty ostre
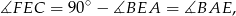
więc są podobne. Stąd
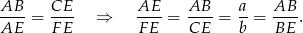
Otrzymana równość oznacza, że przyprostokątne w trójkątach prostokątnych 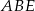 i
i 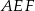 są proporcjonalne, więc trójkąty te są podobne i
są proporcjonalne, więc trójkąty te są podobne i 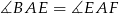
Sposób III
Przedłużmy odcinek 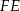 do jego punktu przecięcia
do jego punktu przecięcia 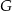 a przedłużeniem odcinka
a przedłużeniem odcinka 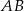 . Zauważmy, że trójkąty
. Zauważmy, że trójkąty 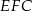 i
i 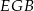 są oba prostokątne i mają wspólny kąt wierzchołkowy, więc są podobne. Ponadto
są oba prostokątne i mają wspólny kąt wierzchołkowy, więc są podobne. Ponadto 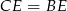 , więc trójkąty te są przystające. W szczególności
, więc trójkąty te są przystające. W szczególności 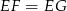 , co z kolei oznacza, że prosta
, co z kolei oznacza, że prosta 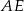 jest jednocześnie wysokością i symetralną boku w trójkącie
jest jednocześnie wysokością i symetralną boku w trójkącie 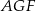 . Jest to więc oś symetrii tego trójkąta, co oznacza, że trójkąt ten jest równoramienny. Prosta
. Jest to więc oś symetrii tego trójkąta, co oznacza, że trójkąt ten jest równoramienny. Prosta 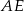 jest więc również dwusieczną kąta
jest więc również dwusieczną kąta 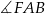 , skąd
, skąd 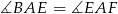 .
.
Sposób IV
Tym razem przedłużmy odcinek 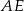 do jego punktu przecięcia
do jego punktu przecięcia 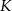 z przedłużeniem odcinka
z przedłużeniem odcinka 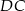 .
.
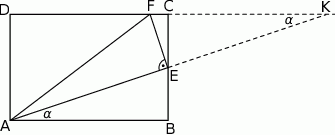
Zauważmy, że trójkąty 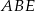 i
i 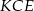 oba są prostokątne i mają równe kąty ostre:
oba są prostokątne i mają równe kąty ostre: 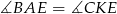 . Ponadto
. Ponadto 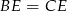 , więc trójkąty te są przystające. W szczególności
, więc trójkąty te są przystające. W szczególności 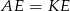 , co z kolei oznacza, że prosta
, co z kolei oznacza, że prosta 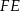 jest jednocześnie wysokością i symetralną boku w trójkącie
jest jednocześnie wysokością i symetralną boku w trójkącie 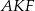 . Jest to więc oś symetrii tego trójkąta, co oznacza, że trójkąt ten jest równoramienny. W takim razie
. Jest to więc oś symetrii tego trójkąta, co oznacza, że trójkąt ten jest równoramienny. W takim razie