Zadanie nr 2130748
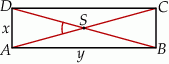
Dany jest prostokąt 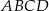 , którego boki mają długości
, którego boki mają długości  i
i 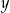 . Punkt
. Punkt 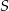 jest punktem przecięcia się przekątnych prostokąta.
jest punktem przecięcia się przekątnych prostokąta.
- Wykaż, że pole trójkąta
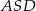 jest cztery razy mniejsze od pola prostokąta
jest cztery razy mniejsze od pola prostokąta 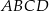 .
. - Wiedząc dodatkowo, że
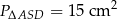 i
i 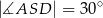 , oblicz pole kwadratu, którego bok ma długość
, oblicz pole kwadratu, którego bok ma długość 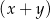 .
.
Rozwiązanie
- Trójkąty
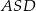 i
i 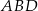 mają wspólną podstawę
mają wspólną podstawę 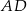 , a wysokość opuszczona na tę postawę w trójkącie
, a wysokość opuszczona na tę postawę w trójkącie 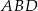 jest dwa razy dłuższa o wysokości opuszczonej w trójkącie
jest dwa razy dłuższa o wysokości opuszczonej w trójkącie 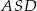 . Zatem
. Zatem 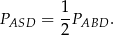
Trójkąt
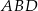 jest jednak połową prostokąta, więc
jest jednak połową prostokąta, więc 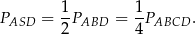
- Zobaczmy co mamy wyliczyć
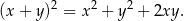
Iloczyn
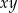 jest równy polu prostokąta, więc z poprzedniego podpunktu mamy
jest równy polu prostokąta, więc z poprzedniego podpunktu mamy 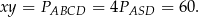
Z drugiej strony,
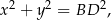
więc pozostało nam wyliczyć długość przekątnej.
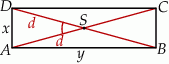
Jeżeli oznaczymy
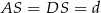 , to ze wzoru na pole trójkąta z sinusem mamy
, to ze wzoru na pole trójkąta z sinusem mamy 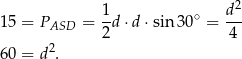
Zamiast stosować wzór na pole trójkąta z sinusem, mogliśmy też zastosować wzór na pole równoległoboku z długościami przekątnych i sinusem.
Mamy więc
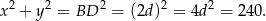
Stąd
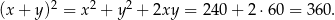
Odpowiedź: