/Szkoła średnia/Geometria/Planimetria/Czworokąt/Prostokąt/Udowodnij

Zadanie nr 3492212

W prostokącie, którego krótszy bok ma długość 8 zawarty jest kwadrat o boku równym różnicy

PIC

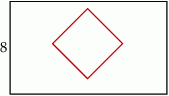
długości boków prostokąta, i którego przekątne są równoległe do boków prostokąta.

  • Wyraź pole pozostałe po wycięciu kwadratu z prostokąta jako funkcję dłuższego boku prostokąta. Wyznacz dziedzinę otrzymanej funkcji.
  • Wykaż, że różnica pól prostokąta i kwadratu jest zawsze większa od 64.
Wersja PDF

Rozwiązanie

  • Oznaczmy długość dłuższego boku prostokąta przez x .
    PIC

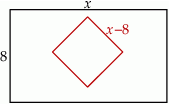
    Szukane pole obliczamy odejmując od pola prostokąta pole kwadratu.

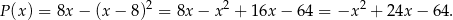
    2 2 2 P (x) = 8x − (x − 8 ) = 8x − x + 16x − 64 = −x + 24x − 64.

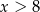    Skoro x ma być dłuższym bokiem prostokąta, musi być x > 8 . Z drugiej strony, przekątna kwadratu nie może być dłuższa od boku prostokąta, czyli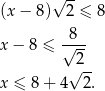

    √ -- (x − 8) 2 ≤ 8 x − 8 ≤ √8-- 2 x ≤ 8+ 4√ 2.

     
    Odpowiedź: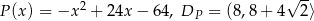 √ -- P(x) = −x 2 + 2 4x− 64, DP = (8,8+ 4 2⟩

  •  

    Sposób I

    Rozwiążmy nierówność

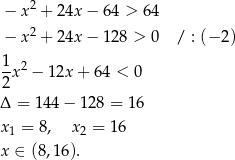
    − x2 + 24x − 6 4 > 64 − x2 + 24x − 1 28 > 0 / : (− 2) 1 -x2 − 12x + 64 < 0 2 Δ = 144 − 12 8 = 16 x = 8, x = 1 6 1 2 x ∈ (8 ,16).

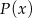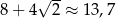    Wystarczy teraz zauważyć, że dziedzina funkcji P(x) jest zawarta w powyższym zbiorze, a to jest oczywiste, bo √ -- 8+ 4 2 ≈ 13,7 .

    Sposób II

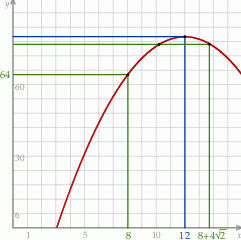
    Zauważmy, że pierwsza współrzędna wierzchołka paraboli będącej wykresem 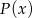P(x ) jest równa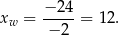

    − 24 xw = -−-2-= 12.

    Zatem funkcja 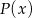P(x) rośnie na lewo od 12 i maleje na prawo od 12. Ponadto 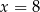x = 8 jest dalej od wierzchołka niż 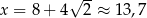√ -- x = 8+ 4 2 ≈ 13,7 . Zatem wartości funkcji 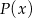P(x ) na przedziale 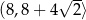√ -- (8 ,8+ 4 2⟩ są nie mniejsze niż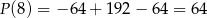

    P (8) = − 64 + 192 − 64 = 64

    (wygodnie jest naszkicować sobie wykres).

    PIC
Wersja PDF