Zadanie nr 9316669
Uzasadnij, że jeżeli prostokąt 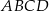 nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.
nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.

Rozwiązanie
Dorysujmy dwusieczne prostokąta.
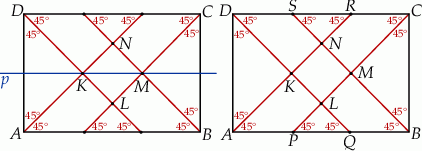
Zauważmy, że każdy z trójkątów 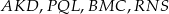 ma dwa kąty równe
ma dwa kąty równe 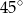 , więc są prostokątne i równoramienne. To oznacza, że każdy z kątów czworokąta
, więc są prostokątne i równoramienne. To oznacza, że każdy z kątów czworokąta 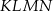 jest prosty, jest to więc prostokąt. Pozostało wykazać, że tak naprawdę jest to kwadrat.
jest prosty, jest to więc prostokąt. Pozostało wykazać, że tak naprawdę jest to kwadrat.
Sposób I
Zauważmy, że prosta 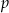 przechodząca przez środki boków
przechodząca przez środki boków 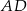 i
i 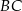 prostokąta jest osią symetrii całego narysowanego obrazka, tzn. przy symetrii względem tej prostej na siebie przechodzi zarówno prostokąt, jak i jego dwusieczne. Ponadto prosta ta zwiera przekątną
prostokąta jest osią symetrii całego narysowanego obrazka, tzn. przy symetrii względem tej prostej na siebie przechodzi zarówno prostokąt, jak i jego dwusieczne. Ponadto prosta ta zwiera przekątną 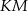 prostokąta
prostokąta 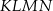 . To oznacza, że jest to także oś symetrii tego prostokąta. To koniec, bo prostokąt, w którym przekątna jest osią symetrii musi być kwadratem.
. To oznacza, że jest to także oś symetrii tego prostokąta. To koniec, bo prostokąt, w którym przekątna jest osią symetrii musi być kwadratem.
Sposób II
Pokażemy, że dwa sąsiednie boki prostokąta 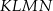 są równe, co będzie oznaczało, że musi to być kwadrat.
są równe, co będzie oznaczało, że musi to być kwadrat.
Zauważmy, że trójkąty 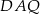 i
i 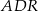 są przystające (bo oba mają równe kąty i wspólny bok
są przystające (bo oba mają równe kąty i wspólny bok 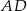 ). Zatem
). Zatem 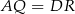 . To oznacza, że
. To oznacza, że 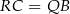 . Analogicznie pokazujemy, że
. Analogicznie pokazujemy, że 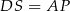 . Mamy więc
. Mamy więc
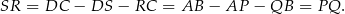
To z kolei oznacza, że trójkąty 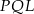 i
i 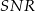 są przystające. Mamy zatem
są przystające. Mamy zatem
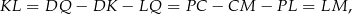
co kończy dowód.
Sposób III
Tak jak poprzednio zauważamy, że 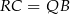 . Teraz patrzymy na równoległoboki
. Teraz patrzymy na równoległoboki 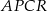 i
i 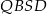 . Mają one równe kąty i równe długości boków, co oznacza, że są przystające. W takim razie mają równe wysokości, czyli
. Mają one równe kąty i równe długości boków, co oznacza, że są przystające. W takim razie mają równe wysokości, czyli